About
I am a final year PhD student in the Networks & Optimization group at CWI working on combinatorial algorithms on strings and graphs under the supervision of Solon Pissis and Leen Stougie as part of the research programme NETWORKS.
Previously, I did my BA in mathematics at the University of Cambridge and my MSc in mathematics at ETH Zürich.
I will soon start a Postdoc in the Algorithms and Complexity group at the Max Planck Institute for Informatics.
Research++
My research interests include algorithms, combinatorics and optimization and their interplay with different fields such as data mining, bioinformatics and machine learning. Click on the buttons below to find out about individual projects. More detailed descriptions and sources can be found in the papers at the bottom of each section.

String Sanitization
Sequential Data
A large number of applications, in domains ranging from transportation to web analytics and bioinformatics feature data modelled as strings, i.e. sequences of letters over some finite alphabet. For instance, a string may represent the history of visited locations of one or more individuals, with each letter corresponding to a location. Similarly, it may represent the history of search query terms of one or more web users, with letters corresponding to query terms, or a medically important part of the DNA sequence of a patient, with letters corresponding to DNA bases. Analyzing such strings is key in applications including location-based service provision, product recommendation, and DNA sequence analysis. Therefore, such strings are often disseminated beyond the party that has collected them.
String Sanitization
However, disseminating a string intact may result in the exposure of confidential knowledge. Thus, it may be necessary to sanitize a string prior to its dissemination, so that confidential knowledge is not exposed. At the same time, it is important to preserve the utility of the sanitized string, so that data protection does not outweigh the benefits of disseminating the string to the party that disseminates or analyzes the string, or to society at large. For example, a retailer should still be able to obtain actionable knowledge in the form of frequent patterns from the marketing agency that analyzed their outsourced data; and researchers should still be able to perform analyses such as identifying significant patterns in DNA sequences.
Combinatorial String Dissemination Model
Motivated by the discussion above, we introduce the following model which we call Combinatorial String Dissemination (CSD). In CSD, a party has a string W that it seeks to disseminate while satisfying a set of constraints and a set of desirable properties. For instance, the constraints aim to capture privacy requirements and the properties aim to capture data utility considerations (e.g., posed by some other party based on applications). To satisfy both, W must be transformed into another string by applying a sequence of edit operations. The computational task is to determine this sequence of edit operations so that the transformed string satisfies the desirable properties subject to the constraints. Clearly, the constraints and the properties must be specified based on the application. In our research, we have designed sanitization algorithms for various natural classes of privacy constraints and utility properties.
Publications
Combinatorial Algorithms for String Sanitization
By Giulia Bernardini, Huiping Chen, Alessio Conte, Roberto Grossi, Grigorios Loukides, Nadia Pisanti, Solon P. Pissis, Giovanna Rosone and Michelle Sweering
ACM Transactions on Knowledge Discovery from Data (TKDD) • Volume 15 • Issue 1 • February 2021.
String Sanitization Under Edit Distance
By Giulia Bernardini, Huiping Chen, Grigorios Loukides, Nadia Pisanti, Solon P. Pissis, Leen Stougie, Michelle Sweering
31st Annual Symposium on Combinatorial Pattern Matching (CPM) • June 2020
String Sanitization Under Edit Distance: Improved and Generalized
By Takuya Mieno, Solon P. Pissis, Leen Stougie and Michelle Sweering
32nd Annual Symposium on Combinatorial Pattern Matching (CPM) • June 2021
Hide and Mine in Strings: Hardness and Algorithms
By Giulia Bernardini, Alessio Conte, Garance Gourdel, Roberto Grossi, Grigorios Loukides, Nadia Pisanti, Solon P. Pissis, Giulia Punzi, Leen Stougie and Michelle Sweering
2020 IEEE International Conference on Data Mining (ICDM) • November 2020
Hide and Mine in Strings: Hardness, Algorithms, and Experiments
By Giulia Bernardini, Alessio Conte, Garance Gourdel, Roberto Grossi, Grigorios Loukides, Nadia Pisanti, Solon P. Pissis, Giulia Punzi, Leen Stougie and Michelle Sweering
IEEE Transactions on Knowledge and Data Engineering (TKDE) • March 2022
Poster

Graph Sanitization
Network Communities
Graphs naturally model relationships between entities in a multitude of domains such as social networks, communication networks, or the web. A fundamental data analysis task in these domains is community detection (i.e., the identification of cohesive or dense subgraphs of a given graph), which employs different notions of graph community; these include the notions of k-plex, n-clan, n-club, k-core, k-ECC, and k-truss. These notions relax the classic notion of clique (i.e., the ideal situation, where all nodes are pairwise connected), either to capture practical application considerations or to enable more efficient enumeration. Regardless of the community notion, the community structure is a key property of a graph. It is therefore essential to study how such a structure can be maintained or broken.
Community Breaking
Here we investigate the following general problem.
Community Breaking (CB) problem: Given an undirected graph G, a subset of its nodes U, and a notion of community, identify the smallest subset of edges such that after removing these edges no community contains a node in U.
The CB problem is motivated by the following real-world applications:
- Maintaining communities in social networks. The edges identified in the output of CB correspond to critical edges for maintaining user engagement in communities.
- Assessing resilience to attacks or errors in communication networks. The edges identified in the output of CB correspond to vital connections in the network.
- Enabling social network users to hide friendships, so that they are not seen as belonging to communities that could lead to their discrimination or unwanted targeted advertisement (e.g., through friend-based profile attribute inference attacks). The edges identified in the output of the CB problem correspond to friendships users could opt to hide.
- Preventing the detection of confidential communities by sanitizing a graph prior to its dissemination, in the spirit of sanitization works on transaction or sequential data. The edges identified in the output of the CB problem must be removed to hide these communities in the sanitized graph.
Identifying a small edge subset is natural yet crucial. For example, in A and B, it allows less costly maintenance of user engagement and network infrastructure improvements, respectively. In C and D, it allows less effort from users and a more accurate analysis of the sanitized graph, respectively.
Publication
On Breaking Truss-Based Communities
By Huiping Chen, Alessio Conte, Roberto Grossi, Grigorios Loukides, Solon P. Pissis and Michelle Sweering
Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining (KDD) • August 2021.
Elastic-Degenerate Strings
Uncertainty in sequences
String matching (or pattern matching) is a fundamental task in computer science. It consists in finding all occurrences of a short string, known as the pattern, in a longer string, known as the text. Many representations have been introduced over the years to account for unknown or uncertain letters in the pattern or in the text, a phenomenon that often occurs in real data. In the context of computational biology, for example, the IUPAC notation is used to represent locations of a DNA sequence for which several alternative nucleotides are possible. Such a notation can encode the consensus of a population of DNA sequences in a gapless multiple sequence alignment.
Elastic-degenerate strings
Iliopoulos et al. generalized these representations to also encode insertions and deletions (gaps) occurring in multiple sequence alignments by introducing the notion of elastic-degenerate strings. Elastic degenerate strings consist of a sequence of sets of strings, where each set describes all variations at that location. We say a string S matches an elestic-degenerate string T if it can be obtained by picking one string from each set in T. Below you can find an example of a multiple sequence alignment and an elastic-degenerate string matching all three of its strings (with the first match illustrated in blue).
GTTCAGTTTACACAA
GTTGAGATT----AA
We have studied the elastic-degenerate string matching problem, which consists in reporting all occurrences of a pattern of length m in an elastic-degenerate text.
Publication
Elastic-Degenerate String Matching with 1 Error
By Giulia Bernardini, Estéban Gabory, Solon P. Pissis, Leen Stougie, Michelle Sweering and Wiktor Zuba
Latin American Symposium on Theoretical Informatics (LATIN) • October 2022
String Sampling
Minimizers
The minimizers sampling mechanism is a popular mechanism for string sampling introduced independently by Schleimer et al. [SIGMOD 2003] and by Roberts et al. [Bioinf. 2004]. Given two positive integers w and k, it selects the lexicographically smallest length-k substring in every fragment of w consecutive length-k substrings (in every sliding window of length w + k − 1).
Example 1. The set Mw,k of minimizers for w = k = 3 for string T = aabaaabcbda (using a 1-based index) is M3,3(T) = {1, 4, 5, 6, 7} and for string Q = abaaa is M3,3(Q) = {3}. Indeed Q occurs at position 2 in T; and Q and T[2 . . 6] have the minimizers 3 and 4, respectively, which both correspond to string aaa of length k = 3.
Minimizers samples are approximately uniform, locally consistent, and computable in linear time. Although they do not have good worst-case guarantees on their size, they are often small in practice. They thus have been successfully employed in several string processing applications. Two main disadvantages of minimizers sampling mechanisms are: first, they also do not have good guarantees on the expected size of their samples for every combination of w and k; and, second, indexes that are constructed over their samples do not have good worst-case guarantees for on-line pattern searches.
bd-Anchors
To alleviate these disadvantages, we introduce bidirectional string anchors (bd-anchors), a new string sampling mechanism. Given a positive integer l, our mechanism selects the lexicographically smallest rotation in every length-l fragment (in every sliding window of length l).Example 2. The set Al of bd-anchors for l = 5 for string T = aabaaabcbda (using a 1-based index) is A5(T) = {4, 5, 6, 11} and for string Q = abaaa, A5(Q) = {3}. Indeed Q occurs at position 2 in T; and Q and T[2 . . 6] have the bd-anchors 3 and 4, respectively, which both correspond to the rotation aaaab.
We show that bd-anchors samples are also approximately uniform, locally consistent, and computable in linear time. In addition, our experiments using several datasets demonstrate that the bd-anchors sample sizes decrease proportionally to l; and that these sizes are competitive to or smaller than the minimizers sample sizes using the analogous sampling parameters. We provide theoretical justification for these results by analyzing the expected size of bd-anchors samples. As a negative result, we show that computing a total order ≤ on the input alphabet, which minimizes the bd-anchors sample size, is NP-hard.
We also show that by using any bd-anchors sample, we can construct, in near-linear time, an index which requires linear (extra) space in the size of the sample and answers on-line pattern searches in near-optimal time. We further show, using several datasets, that a simple implementation of our index is consistently faster for on-line pattern searches than an analogous implementation of a minimizers-based index [Grabowski and Raniszewski, Softw. Pract. Exp. 2017].
Finally, we highlight the applicability of bd-anchors by developing an efficient and effective heuristic for top-K similarity search under edit distance. We show, using synthetic datasets, that our heuristic is more accurate and more than one order of magnitude faster in top-K similarity searches than the state-of-the-art tool for the same purpose [Zhang and Zhang, KDD 2020].
Preprint
String Sampling with Bidirectional String Anchors
By Grigorios Loukides, Solon P. Pissis and Michelle Sweering.
Code available in C++.
Connecting Strings
De Bruijn Graphs
The order-k de Bruijn graph (dBG) of a collection S of strings is a directed multigraph GS,k(V, E) such that
- V is the set of length-(k − 1) substrings of the strings in S and
- GS,k contains an edge (u, v) with multiplicity mu,v if and only if the string u[0] · v is equal to the string u · v[k − 2] and this string occurs exactly mu,v times in total in strings in S.
Computing a string which contains a set of given substrings arises naturally as an encoding problem in many other contexts as well, such as data privacy and data compression. Depending on the application, we may or may not require the order and/or frequency of the substrings to be preserved. Moreover, we may want to avoid occurrences of specific forbidden patterns modelling confidential knowledge.
Publications
Making de Bruijn Graphs Eulerian
By Giulia Bernardini, Huiping Chen, Grigorios Loukides, Solon P. Pissis, Leen Stougie and Michelle Sweering
33rd Annual Symposium on Combinatorial Pattern Matching (CPM) • June 2022
Code available in C++.
On Strings Having the Same Length-k Substrings
By Giulia Bernardini, Alessio Conte, Estéban Gabory, Roberto Grossi, Grigorios Loukides, Solon P. Pissis, Giulia Punzi and Michelle Sweering
33rd Annual Symposium on Combinatorial Pattern Matching (CPM) • June 2022
Constructing Strings Avoiding Forbidden Substrings
By Giulia Bernardini, Alberto Marchetti-Spaccamela, Solon P. Pissis, Leen Stougie and Michelle Sweering
32nd Annual Symposium on Combinatorial Pattern Matching (CPM) • June 2021
Periodicity
Borders and periods
A word can overlap itself if one of its prefixes is equal to one of its suffixes. The corresponding prefix (or suffix) is called a border and the shift needed to match the prefix to the suffix is called a period. For example, consider the word abracadabra: then, abra is its longest border of abracadabra and corresponds to a period of 7, but a is also a border of abracadabra corresponding to a period of 10, and finally, the word abracadabra is a border itself corresponding to a trivial period of 0. Importantly, a period is an offset at which two occurrences of a word w can overlap themselves.
01234567890..........
abracadabra----------
-------abracadabra---
----------abracadabra
The notions of borders and periods are key in word combinatorics, in stringology, and especially in pattern matching algorithms. The set of periods of a word impacts how occurrences of this word can appear in random texts.
Autocorrelations
Consider words of length n. The set of all periods a word of length n is a subset of {0, 1, 2, . . . , n−1}. However, any subset of {0, 1, 2, . . . , n−1} is not necessarily a valid set of periods. In a seminal paper in 1981, Guibas and Odlyzko proposed to encode the set of periods of a word into an n-long binary string, called autocorrelation, where a 1 at position i denotes a period of i (revisiting the example above, the string abracadabra has period set {0, 7, 10} and autocorrelation 10000001001). They considered the question of recognizing a valid period set, and also studied the number of valid period sets for length n, denoted κn. They conjectured that ln(κn) asymptotically converges to a constant times ln2(n). If improved lower bounds for ln(κn) / ln2(n) were proposed in 2001 by Rivals and Rahmann, the question of a tight upper bound has remained open since Guibas and Odlyzko’s paper.
In our paper, we exhibit an asymptotically matching upper bound for this fraction, which implies its convergence, and closes this long-standing conjecture. Moreover, we extend our result to find similar bounds for the number of correlations: a generalization of autocorrelations which encodes the overlaps between two strings.
Preprint
Convergence of the number of period sets in strings
By Eric Rivals, Michelle Sweering and Pengfei Wang.
50th EATCS International Colloquium on Automata, Languages and Programming (ICALP) • July 2023
Poster

Online Graph Problems
Online graph problems are among the most fundamental online optimization problems, where an initially unknown input is revealed incrementally. The two main paradigms for incremental information release are the online-time model and the online-list model. In the online-time model, initially unknown requests are revealed over time and can be served at any time, whereas in the online-list model, requests are revealed one by one and must be served immediately before the next request appears.
In our work, we address specifically the following online routing and network design problems.
- Online-time routing problems. In the classical Online Traveling Salesperson Problem (OLTSP) and Online Dial-a-Ride Problem (OLDARP), a server can move at unit speed in a given metric space. Transportation requests appear online over time, each defining a start and end point in the metric space (in the TSP both points are equal). The task is to determine a tour to serve all requests (in any order) by moving to the corresponding start and end points. The objective is to minimize the makespan, i.e., the time point when all requests have been served and the server is back in the origin.
- Online-list network design problems. In the Online Steiner Tree Problem, requests are terminal nodes that are revealed one by one in a given metric space (typically represented as a complete edge-weighted graph) and must be connected to a fixed root by selecting edges via other (Steiner) nodes. In the closely related Online Steiner Forest Problem, a request is composed of two nodes which have to be connected by the selected set of edges. In both problems, the objective is to minimize the total cost of selected edges. In the more general Online Facility Location Problem, a facility can be opened at every vertex at a certain one-time cost at any time, and arriving client vertices are connected upon arrival to the closest open facility at the cost of the shortest path to it. The goal is to minimize the opening and connection cost.
The performance of online algorithms is typically assessed by worst-case analysis. An algorithm is called ρ-competitive if it computes, for any input instance, a solution with objective value within a multiplicative factor ρ of the optimal value that can be computed when knowing the full instance upfront. The competitive ratio of an algorithm is the smallest factor ρ for which it is ρ-competitive.
For the above problems (nearly) tight bounds on the competitive ratio are known. For OLTSP and OLDARP, there have been shown best possible 2-competitive algorithms. For the online network design problems, the existence of O(1)-competitive algorithms has been ruled out and algorithms with (tight) (poly-)logarithmic upper bounds have been shown.
Learning Augmented Algorithms
The assumption in online optimization of not having any prior knowledge about future requests seems overly pessimistic. In particular, given the success of machine-learning methods and data-driven applications, one may expect to have access to predictions about future requests. However, simply trusting such predictions might lead to very poor solutions, as these predictions come with no quality guarantee. The recent vibrant line of research aims at incorporating such error-prone predictions into online algorithms, to go beyond worst-case barriers. The goal is to design learning-augmented algorithms with a performance that is close to that of an optimal online algorithm when given accurate predictions (called consistency) and, at the same time, never being (much) worse than that of a best-known algorithm without access to predictions (called robustness). Further, the performance of an algorithm shall degrade in a controlled way with increasing prediction error.
We developed a novel measure for quantifying the error in input predictions and apply it to derive error-dependent performance guarantees of algorithms for online metric graph problems.
Publication
A Universal Error Measure for Input Predictions Applied to Online Graph Problems
By Giulia Bernardini, Alexander Lindermayr, Alberto Marchetti-Spaccamela, Nicole Megow, Leen Stougie and Michelle Sweering
Thirty-sixth Conference on Neural Information Processing Systems (NeurIPS) • December 2022
Poster

Bipartite Networks in Ecology
Bipartite networks are widely used to represent a diverse range of species interactions, such as pollination, herbivory, parasitism and seed dispersal. The structure of these networks is usually characterised by calculating one or more indices that capture different aspects of network architecture. While these indices capture useful properties of networks, they are relatively insensitive to changes in network structure. Consequently, variation in ecologically-important interactions can be missed. Network motifs are a way to characterise network structure that is substantially more sensitive to changes in pairwise interactions and is gaining in popularity.
However, there is no software available in R, the most popular programming language among ecologists, for conducting motif analyses in bipartite networks. Similarly, no mathematical formalisation of bipartite motifs has been developed.
bmotif
We introduce bmotif: a package for motif analyses of bipartite networks. Our code is primarily an R package, but we also provide MATLAB and Python code of the core functionality. The software is based on a mathematical framework where, for the first time, we derive formal expressions for motif frequencies and the frequencies with which species occur in different positions within motifs. This framework means that analyses with bmotif are fast, making motif methods compatible with the permutational approaches often used in network studies, such as null model analyses.
We describe the package and demonstrate how it can be used to conduct ecological analyses, using two examples of plant-pollinator networks. We first use motifs to examine the assembly and disassembly of an Arctic plant-pollinator community and then use them to compare the roles of native and introduced plant species in an unrestored site in Mauritius.
bmotif will enable motif analyses of a wide range of bipartite ecological networks, allowing future research to characterise these complex networks without discarding important mesoscale structural detail.
Publication
bmotif: A package for motif analyses of bipartite networks
By Benno I. Simmons, Michelle J. M. Sweering, Maybritt Schillinger, Lynn V. Dicks, William J. Sutherland and Riccardo Di Clemente.
Methods in Ecology and Evolution (MEE). 2019; 10: 695– 701.
Code available in R, Python 2 and MATLAB.
Poster
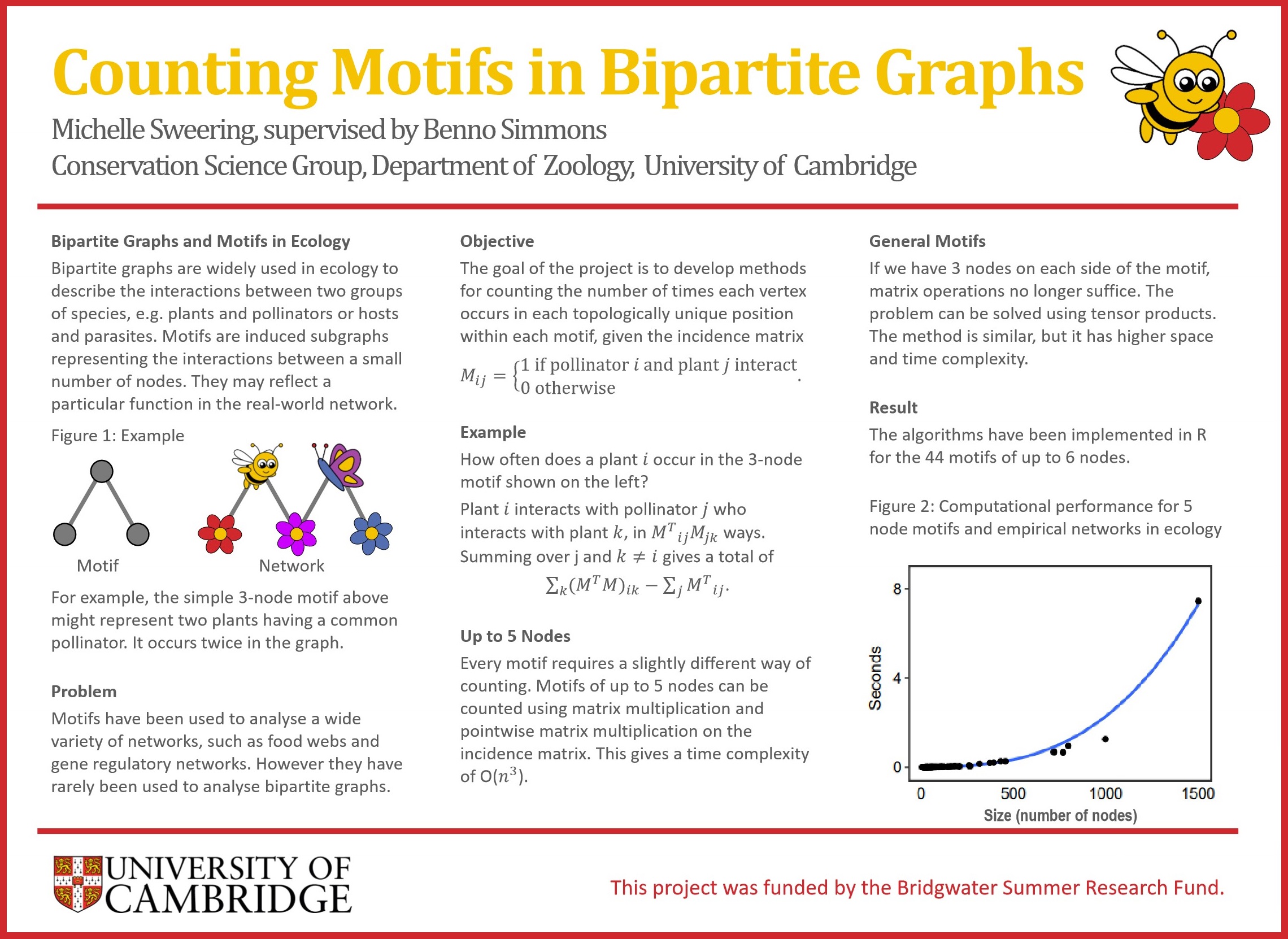
Covering Problems in Hypergraphs
Many combinatorial problems can be formulated as finding the cover number of a certain hypergraph. Unfortunately, determining the cover number of hypergraphs is in many cases extremely difficult. For my master thesis, I studied bounds on the transversal number of r-uniform hypergraphs satisfying a certain natural property called the (k, l)-property.
An r-uniform hypergraph is a hypergraph in which each edge contains exactly r vertices. Such a hypergraph satisfies the (k, l)-covering property, if each k of its edges can be covered using l vertices. Specific regimes of interest include: small l, in particular l = 2, and large l, in particular l = r. A special case of this covering property is directly related to the classical Ryser’s conjecture about the relation between the transversal number and the matching number of r-uniform r-partite hypergraphs.
Example of a tripartite 3-uniform hypergraph. Edges are depicted with ellipses and vertex classes with colours.
Covering Problems in Hypergraphs
Master Thesis written during my MSc Mathematics at ETH Zürich. Supervised by Matija Bucić and Benny Sudakov.
A Combinatorial Perspective on the Log-Rank Conjecture
The log-rank conjecture is a conjecture in communication complexity. So what is communication complexity? Suppose that we have two players, Alice and Bob, say, and a 01-matrix M with m rows and n columns. Now Alice is assigned a row i and Bob is assigned a column j. Both players know what the matrix looks like, but they don’t know which row/column the other player was assigned. What is the maximum number of bits they have to send to each other to figure out the value of Mij?
This is a bit confusing, so let’s illustrate it with an example of such a protocol. Alice could just send Bob her index i as a binary number using O(log(m)) bits. Then Bob looks up the value of Mij in the matrix and can send it to Alice using a single bit. This shows that the communication complexity is at most O(log(m)). This strategy is not necessarily optimal. The number of bits needed to send the choice of row is logarithmic in the number of rows. The same can be achieved for the columns. However, if they work together, they might be able to use the information they get from each other to send information more efficiently, especially if the matrix has some ‘nice’ properties. In our case, we are interested in low-rank matrices. This leads us to the log-rank conjecture, which was first formulated by Lovász and Saks in 1988.
The log-rank conjecture states that the communication complexity of a 01-matrix is polylogarithmic in its rank. This is related to graph theory since we can bound the logarithm of the chromatic number of a graph by the communication complexity of its adjacency matrix. This semester paper gives an overview of results in the area, focusing on the most recent upper bound by Lovett.
A Combinatorial Perspective on the Log-Rank Conjecture
Semester Paper written during my MSc Mathematics at ETH Zürich. Supervised by Matija Bucić and Benny Sudakov.
Ramsey Numbers of Hypercubes
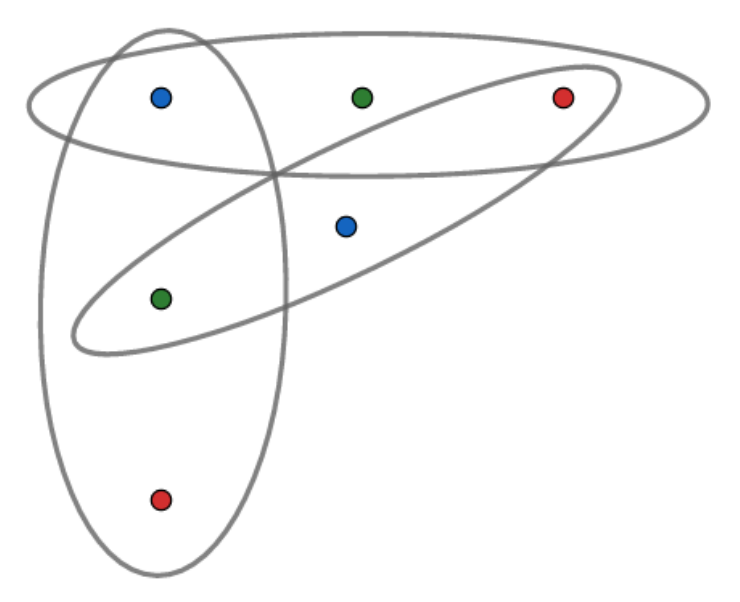
This essay is about Ramsey theory. Ramsey theory is a branch of graph theory looking for order in disorder. A graph is a set of points, the vertices, joined by some lines, the edges. If there is an edge between each pair of vertices, we say the graph is complete. We denote the complete graph on n vertices with Kn. Now suppose we colour each edge of Kn either red or blue. Can we find patterns in this? Can we find a blue triangle? What about a red triangle? It turns out that if you have six vertices you can always find one of them.
Instead of searching for red or blue triangles, we could consider a different pair of graphs, one completely red and one completely blue. Can we always find one of the two, if we search a sufficiently large complete graph? Ramsey’s theorem says we can.
As you can see K5 need not contain a red or blue triangle. For K6 we failed to find such an arrangement. Can you see why?
Ramsey’s Theorem. Consider a blue graph G1 and a red graph G2, then there exists N such that every red-blue-colouring of a complete graph of size N contains one of the two. The minimal such N called is the Ramsey number of G1 and G2.
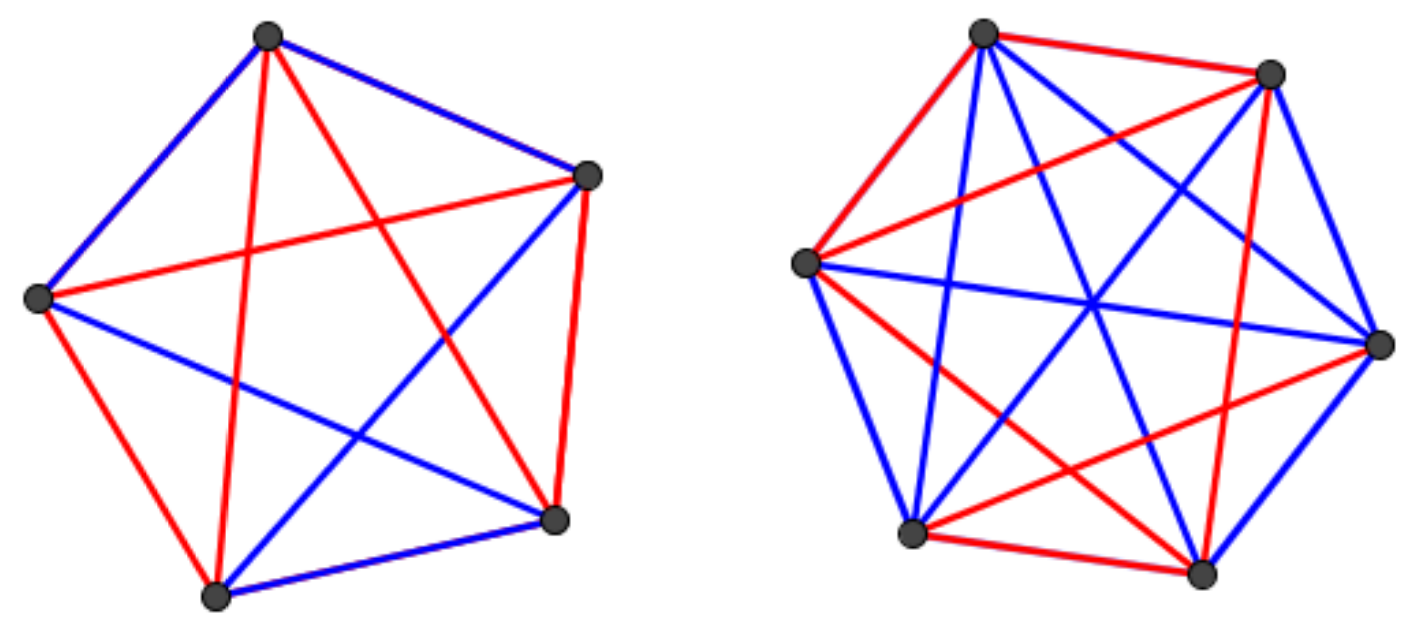
There are plenty of other subgraphs of interest besides cliques. However, we consider a particularly important one: the hypercube. Hypercubes play a key role as they are the graphical interpretation of powersets. The n-dimensional hypercube has its vertices labelled by elements of {0, 1}n with edges joining them if and only if their labels only differ in one coordinate.
Problem. What is the value of R(Qn, Ks), the Ramsey number of the red hypercube of dimension n and the blue clique on s vertices?
In this essay, we discuss various results from the literature including lower and upper bounds which together determine the exact Ramsey number for n sufficiently large, as well as a generalization of this result where the red hypercubes are paired with arbitrary blue graphs.
Ramsey Numbers of Hypercubes
Mathematical Essay written during my BA Mathematics at Trinity College, Cambridge, which was awarded a Yeats Prize. Topic proposed by Imre Leader.
Je Ongelijk Bewijzen
At the International Mathematical Olympiad 2012 in Argentina, I won an honourable mention by getting full marks for the following problem:
Problem 2. Let n ≥ 3 be an integer, and let a2, a3, . . . , an be positive real numbers such that
a2a3 · · · an = 1. Prove that
In this article, I explain the inequality of arithmetic and geometric means (AM-GM) and how it can be used to solve this problem.
Je Ongelijk Bewijzen (in Dutch)
Popular scientific article for teenagers. Published in Pythagoras Magazine, January 2013.


Contact
Email: msweerin@mpi-inf.mpg.de
Homepage: michellesweering.github.io
LinkedIn: www.linkedin.com/in/michelle-sweering
Papers: ORCID -
Google Scholar -
![]() dblp
dblp